德州扑克跟我学报道:

Modern Poker Theory
现代扑克理论
底牌可玩性(Hand Playability)
如果扑克中没有下注而牌手被迫每手牌都全压,每个牌手的期望值将是他们的底池权益(Equity)乘以底池大小。
EV = EQ * Pot
例子
在一个单挑牌局,每个牌手必须投入100美元前注,但没有任何后续下注。牌手1拿着4♦ 4♠,牌手2拿着9♥ 8♥。每个牌手的预期收益是多少?
4♦ 4♠的底池权益是47.26%。
牌手1的EV = 47.26% x 200 = 94.52美元
9♠ 8♠的底池权益是52.74%。
牌手2的EV = 52.74% x 200 = 105.48美元
在这个假想的玩具游戏中,两个牌手都100%实现了他们的底池权益。然而,在多回合下注的真正扑克游戏中,如果一个牌手在摊牌前弃牌,他放弃了自己的底池权益,将它移交至剩余牌手。这种动态被称为底池权益实现。
底池权益实现(Equity Realization,EqR)
底池权益实现指用EV具体化的底池权益部分。底牌得到超过其底池权益的底池份额被称为过度实现(over-realize)底池权益。底牌得到的底池份额小于它的底池权益被称为底池权益实现不足(under-realize)。
牌例
牌局类型:55美元买入网络9人桌MTT锦标赛
有效筹码量:枪口玩家50BB,大盲玩家40BB
牌手数量:9人(12.5%前注)
翻前:(2.625BB) 枪口位置的常客玩家率先加注到2BB。所有人弃牌,轮到在大盲位置拿着9♣ 5♦的Hero行动,他需要做一个决定。
因为枪口玩家是一个常客玩家,你假定他用一个可以轻松防守3bet的16%起手牌标准范围率先加注(底牌范围12),因此用9♣ 5♦ 3bet诈唬是不可能的。Hero只有跟注和弃牌两种选择。
如果你用所有筹码跟注,解决方案将是简单地比较你的底池赔率和你的底牌胜率(Hand Equity),如果你的底牌胜率大于底池赔率就跟注。
9♣ 5♦对抗枪口玩家范围的胜率是29.5%。
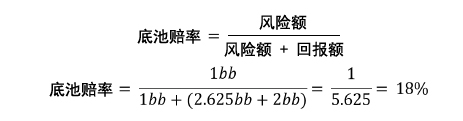
显然你的底牌胜率远好于底池赔率。但是,因为你并非全压,如果你跟注,你将不得不游戏可能出现各种结果的翻后。对手可能很激进,且有时会迫使你放弃更好的牌。对手可能拿到一手比你更强的牌,而且你可能输掉一个大底池。你可能翻牌圈拿到一手强牌,但得不到任何行动,甚至偶尔把所有筹码输给对手。遗憾的是,净胜率(假设你全压的胜率)并没考虑到这些可能性的任何一种。

底牌范围12:包括16%起手牌的枪口位置率先加注范围
如果你不知道你最终遇到哪种局面,你怎么知道你的跟注是否+EV?
底池权益实现因素告诉你对于所有可能局面平均而言你预计能实现多少底池权益。因此,如果你知道你的底牌胜率和底池权益实现因素(EqR),你可以计算包括翻后游戏的更复杂局面的期望值。
跟注的EV = EqR (Eq * Pot)
因此,如果你知道Eq和EV,你可以算出EqR:
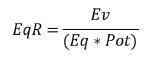
将EV转换成以底池大小为基准的EV:
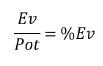
底池权益实现的简化公式是:
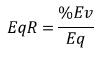
为每个底池计算每手牌的EqR几乎是不可能的,因为这实际上需要具有整个扑克游戏的解决方案。但是,两种方法可以让你得到极好的近似值。
l 你可以从数百万手网络牌局采样出实验数据,将它们的底池权益和它们在每一场合获得的底池份额相比较。
l 你可以利用现代Solver软件获得每手牌在各种场合的EqR,然后将结果取平均值。
底池权益实现热点图
下列底池权益实现热点图(热点图1-4)由Pio Solver生成。它们展示了在短筹码和中筹码场景中大盲玩家在单一加注底池对抗一个前面位置牌手或按钮位置牌手的结果。假定有12.5%的前注。
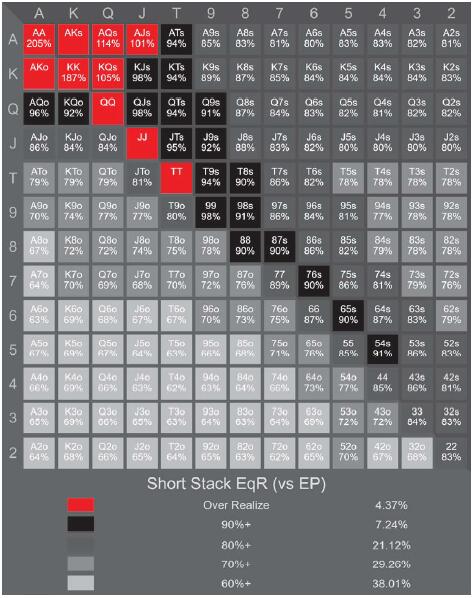
热点图1:对抗前面位置玩家的底池权益实现(10-20BB)
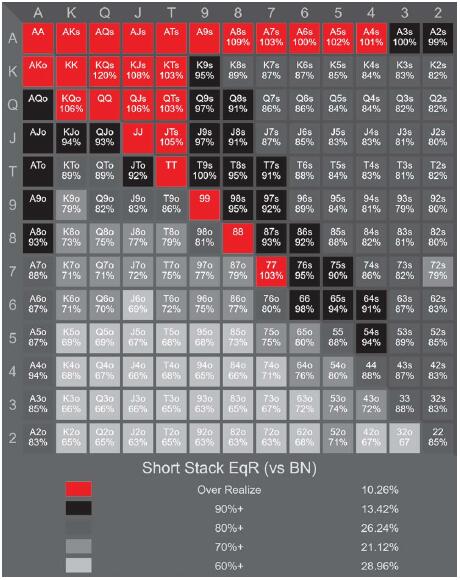
热点图2:对抗按钮玩家的底池权益实现(10-20BB)
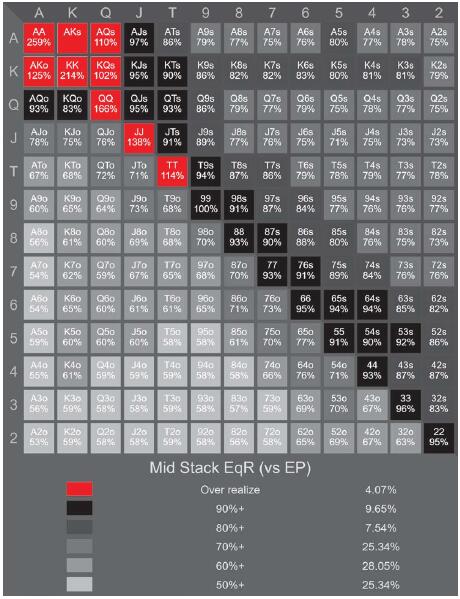
热点图3:对抗前面位置玩家的底池权益实现(30-75BB)
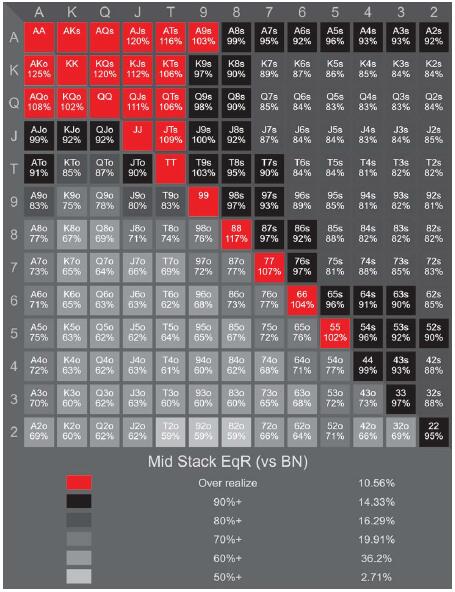
热点图4:对抗按钮玩家的底池权益实现(30-75BB)
回到Hero拿着95o的例子,把热点图3的EqR代入EV公式:
跟注的EV = EqR(Eq * Pot)- Risk
跟注的EV=0.58(0.295 * 4.625)- 1 = -0.21BB
这说明用9♣ 5♦跟注是负期望值的,因此应该弃牌(尽管它其实有足够多的净胜率)。
解决这个问题的另一种方法是,首先找出为使跟注不亏不盈9♣ 5♦需要实现多少底池权益:

9♣ 5♦具有58%的EqR,比61%的最小EqR少3%。这意味着,即使我们有很高的底池权益,我们也无法在翻后实现足够使跟注有利可图的底池权益。
影响底牌可玩性的因素
位置
几乎所有牌手至少在一定程度上知道位置的重要性。从他们开始打牌起,他们就一直被告知避免在不利位置游戏和在有利位置游戏会轻松很多,但他们没被告知的是,为何具有位置优势如此重要。
当你有坐在有利位置时,你具有在牌局的剩余每个回合(street)最后行动的优势,这意味着你可以看到对手在做什么,并能做出相应反应。最重要的是,如果对手check,你可以随后check,保证得到一张免费牌,这造成了有利位置者和不利位置者在底池权益实现方面的巨大差异。在不利位置check后,你往往会遇到一个下注,被迫弃牌,底池权益被剥夺。
牌力(Hand Strength)
如果一手牌具有很高的净胜率,那么底池权益实现变得不那么重要,因为高胜率的牌在大多数场合乐意游戏大底池。它们也提供了许多弹性,因为你可以用它们跟注或加注。
胜率极低的牌也很容易游戏,因为大多数时候正确的玩法是弃牌。
中等牌力的牌是真正难以游戏的牌,它们很想打到摊牌或看一张免费牌,但如果对手施加大量压力,这些牌难以继续游戏。
同花能力(Hand Suitedness)
平均而言,因为兼具前门同花听牌和后门同花听牌的能力,同花牌相比非同花牌多实现16%的底池权益。这给了它们许多弹性,要么更高效地半诈唬,要么用具有较高潜在底池赔率的牌跟注。
连子能力(Hand Connectedness)
像Q2o这样无连子能力的非同花牌属于EqR最低的牌。因为它们翻牌圈要么拿着踢脚糟糕的大对子要么拿着听牌能力有限的小对子。因此,用它们实现底池权益非常困难。
范围优势
在范围对抗中具有胜率优势可以帮助你范围中的较弱牌实现它们的底池权益,因为如果你的范围比对手的范围强,他就无法太激进地下注。这使得你范围中难以承受下注的较弱牌能够看到更多免费牌。
筹码底池比(SPR)
筹码底池比(SPR)是有效筹码量除以底池大小的比值:
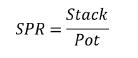
知道你的筹码量相对于底池大小有多大很重要。它允许你提前计划和根据游戏中的范围调整你的下注尺度。表8列出了12.5%前注MTT锦标赛的典型SPR。
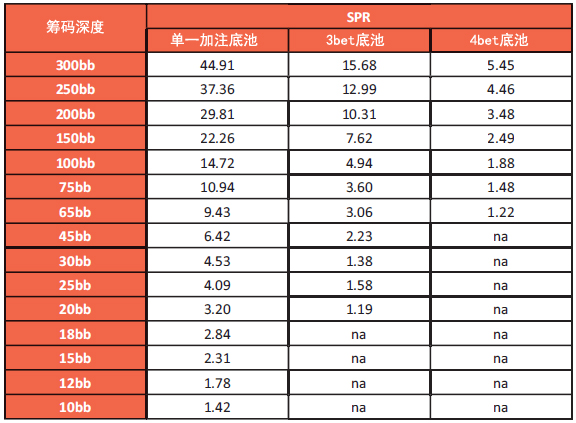
表8:12.5%前注MTT锦标赛的典型SPR
关于SPR的一般准则
l 低SPR(0-5):翻牌圈能拿到顶对、高对这样成手牌的底牌在低SPR场合比投机牌更好游戏。因为投机牌缺乏弃牌赢率,潜在底池赔率较低,难以实现它们的底池权益。
l 中SPR(6-11):顶对类型牌的价值减弱,投机牌的价值上升。底牌的底池权益实现开始与同花能力和连子能力而不是高牌价值(high card value)紧密联系。
l 高SPR(11+):随着筹码量变得越来越深,底牌的价值越来越来自它构成坚果牌的潜力(坚果能力)。像暗三条、坚果听牌、大同花和大顺子这样可能cooler对手的牌价值上升。除非具有某种后备胜率(backup equity),单个对子类型的牌难以在大底池打到摊牌。
范围形态学(Range Morphology)
底牌范围可以根据它们对抗对手范围的胜率分布分类。
线性范围(Linear Range)
线性范围由其间无间隙的胜率最高的牌组成。以下是一个例子(底牌范围13)。
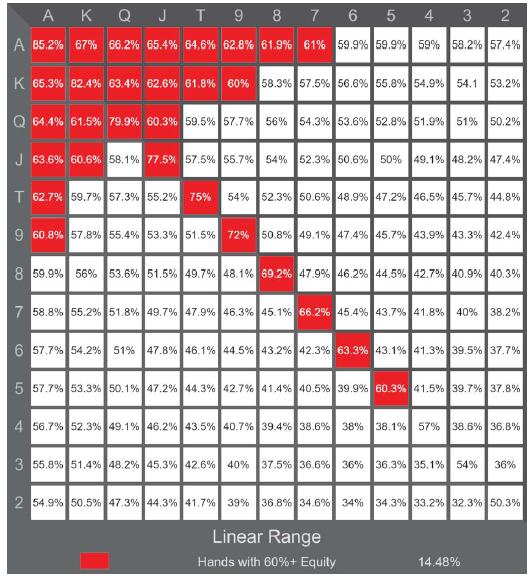
底牌范围13:对抗一手随机牌具有至少60%胜率的牌
两极化范围(Polarized Range)
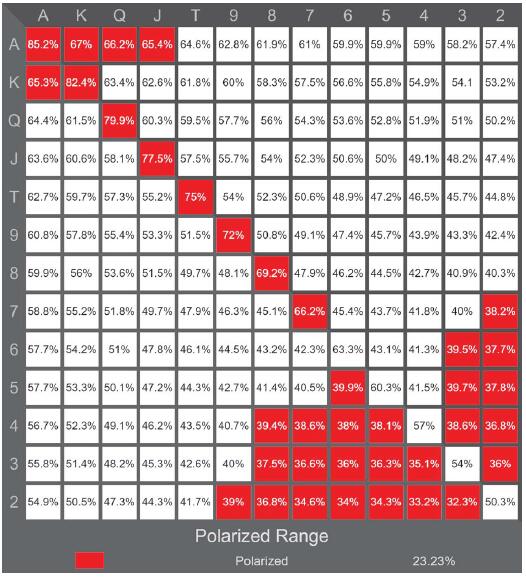
两极化范围由高胜率的价值牌和低胜率的诈唬牌组成。如果一个范围只包括坚果牌和诈唬牌,不包括任何两者之间的牌,它就是完美两极化的。以下是一个例子(底牌范围14)。
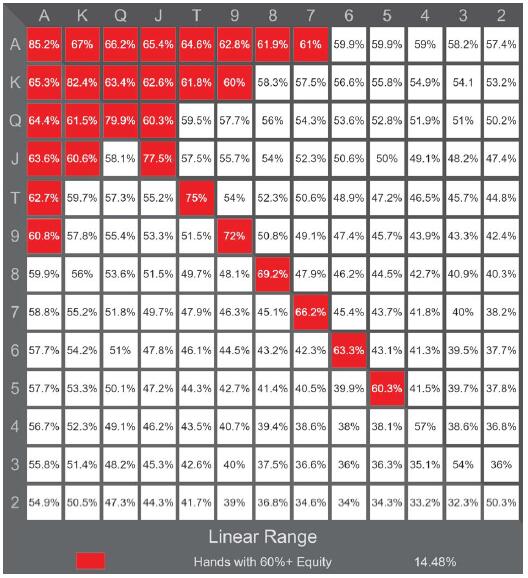
底牌范围14:对抗一手随机牌具有超过65%胜率或不到40%胜率的牌
去两极化范围/紧缩的范围(Depolarized/Condensed Range)
紧缩的范围或去两极化范围是两极化范围的反面。它移除了顶端牌(胜率最高的牌)和底端牌(胜率最低的牌),只由中等胜率牌组成(参见底牌范围15)。
底牌范围15:对抗一手随机牌胜率在40%到65%之间的牌
有上限的/无上限的范围(Capped/Uncapped Range)
当一个范围不存在最强牌(顶端牌)时,它被称为有上限的范围。相反,如果一个范围具有所有最强牌,它被称为无上限的范围。
牌例
牌局类型:219美元买入网络9人桌MTT锦标赛
有效筹码量:按钮玩家25BB,大盲玩家15BB
牌手数量:9人(12.5%前注)
翻前:(2.625BB) 按钮玩家率先加注到2BB,小盲玩家弃牌,大盲玩家跟注。
翻牌圈:(5.625BB)A♥ J♦ T♠
在A♥ J♦ T♠翻牌面,大盲玩家的范围(底牌范围16)缺乏所有坚果牌(比如顺子(KQ)、暗三条(AA、JJ、TT))和大多数两对(AJ、AT),因此这个范围被称为有上限的。相反,按钮玩家的范围(底牌范围17)是无上限的,因为它包括所有这些牌。

底牌范围16:有上限的范围

底牌范围17:无上限的范围
紧缩的范围是有上限的,但有上限的范围未必是紧缩的。例如,如果翻牌是5♥ 4♦ 3♠,那么大盲玩家的范围是紧缩的,但它可能包括很强的牌,比如顺子和两对,因此它不是有上限的。
注意:在真实牌局中范围极少是完美两极化、完美线性或任何其他纯粹的类型。在大多数情况下,它们是各种范围类型的混合体。
天龙扑克,亚洲扑克游戏领导者!天龙扑克注册地址:http://www.tianlongqipai.com
本文由德州扑克跟我学整理发布
 博狗扑克 蜗牛扑克 德州扑克跟我学
博狗扑克 蜗牛扑克 德州扑克跟我学
















