德州扑克跟我学报道:

Modern Poker Theory
现代扑克理论
无偏倚原则(The Indifference Principle)
Will Tipton在其著作《Expert Heads Up No Limit Hold’em,Volumes1:Optimal and Exploitative Strategies》中非常精确地定义了无偏倚原则。
“根据定义,均衡策略在面对一个采用自己的GTO策略的对手时(在这种情况下,对手的每手牌都是以尽可能有利可图的方式游戏)是最大程度剥削策略。因此,一手牌能够以两种不同方式游戏的唯一方式是这两个行动具有恰好相同的EV;也就是说,如果牌手对他的行动选择不偏不倚。这被称作无偏倚原则:如果一个牌手在纳什均衡中采用对一手牌采用一种混合策略,那么他用非零频率采取的所有行动必定具有相同的EV。这是一个有力的声明,因为它告诉我们关于对手GTO策略的一个事实。如果一个牌手对于两种选择不偏不倚,必定是他的对手的游戏方式让他那么做。”
这个原则与平衡思想密切相关。回想我们之前的例子:我们知道按钮玩家的GTO全压范围是58.3%起手牌。他无法用高百分比的起手牌全压是因为大盲玩家跟注足够多,从而按钮玩家无法用他范围的低端部分(比如43s)做有利可图的全压。如果按钮玩家可以用范围的低端部分有利可图地全压,那么他将入继续往他的全压范围加入一些牌。与此同时,如果按钮玩家用43s全压是亏钱的,他将选择不用43s全压,另一些牌将成为其范围的新底端。因此,大盲玩家必须用恰好数量的牌跟注,使得按钮玩家全压范围中的最差牌是不亏不盈的,或者换句话说,使得按钮玩家对于全压和弃牌不偏不倚。因为43s对全压或弃牌不偏不倚,按钮玩家对它采用一种混合策略:74%的时候全压,26%的时候弃牌。如果按钮玩家在超过74%的时候用43s全压,大盲玩家可以通过用更多牌跟注来剥削,使得43s是一手负EV的全压。
与此同时,在纳什均衡中,大盲玩家只能用37.4%的牌有利可图地跟注。他跟注范围的底端(Q6s)是不亏不盈的,而且也采用一种混合策略:39%的时候跟注,61%的时候弃牌。如果大盲玩家用在超过61%的时候用Q6s跟注,按钮玩家可以通过稍紧一点的全压剥削,使得Q6s是一手负EV的跟注牌。
通灵玩具游戏(The Clairvoyance Toy Game)
考虑以下简化扑克场景:
牌例
两个牌手:牌手1和牌手2
底池大小:100美元
有效筹码量:100美元
下注回合:河牌圈
牌手1范围:A♠ A♥,Q♣ Q♦
牌手2范围:K♣ K♦
公共牌:3♠ 3♥ 3♣ 2♦ 2♠
牌手1位置:不利位置
牌手2位置:有利位置
两个牌手是通灵的(clairvoyant):他们知道彼此的策略。
每个牌手的价值是多少?
在这个假想的场景中,牌手1有一个两极化范围。AA代表坚果牌,QQ代表空气牌,因为它对抗牌手2由KK(抓诈牌)组成的紧缩范围无法在摊牌时获胜。
每个牌手的范围的底池权益(equity)是多少?
牌手1在拿着AA的一半时候赢得底池,并在拿着KK的一半时候输掉底池。因此每个牌手在这个底池的底池权益是50%。
如果每个牌手的底池权益是50%而底池有100美元,每个牌手的EV是多少?
谨记,底池权益不考虑翻后玩法,因此,即使两个牌手都有50%底池权益,也未必意味着他们将获得底池的50%。
如我们在解决这个玩具游戏后所见,牌手1的EV事实上是75美元,而牌手2的EV只有25美元,即使两个牌手都完美地游戏!
排除劣势策略(Eliminating Dominated Strategies)
对下注放弃AA
AA总是会获胜,因此用AA跟注一个任何尺度下注的EV是:
用AA跟注的EV = 底池大小 + 下注额 = 100美元 + 下注额
放弃AA的EV = 0
放弃AA明显是一种应该从不使用的劣势策略(Dominated Strategies)。
用QQ跟注下注
放弃QQ的EV = 0
QQ对抗KK永远无法在摊牌时获胜。因此,用QQ跟注一个任何尺度下注的EV是:
用QQ跟注的EV = -下注额
用一种无法获胜的牌跟注一个下注是劣势策略,因此牌手1应该总是对下注放弃QQ,因为不管下注额是多少跟注都是输钱的。
用KK下注或加注
因为牌手1从不放弃AA也从不用QQ跟注,用Kk下注达不到任何目的。当牌手1拿着AA时,下注输掉更多资金,因此用KK下注是一种应该从不使用的劣势策略。
用AA Check
我们知道牌手2从不用KK下注,因此如果牌手1用AA check,牌手2将随后check,牌手1将永远赚不到额外的下注,因此牌手1应该总是用AA下注。
排除所有劣势策略后,这场博弈可以简化成以下几个问题:
l 牌手1的最优下注尺度是什么?
l 牌手1用QQ诈唬的频率是多少?
l 牌手2用KK跟注的频率是多少?
l 如果调换两个牌手的位置会发生什么情况?
牌手1的最优下注尺度是全压。将来我们将论证这一点,但我们暂且假定牌手1的唯一下注尺度是全压。
排除纯粹策略(Ruling Out Pure Strategies)
我们知道牌手1应该总是用AA下注,但QQ应该如何游戏?我们现在开始分析。
纯粹策略A:牌手1总是用QQ诈唬
当牌手1总是用他的QQ诈唬时,牌手2的EV是:
抓诈唬EV = [%W * $W]-[%L * $R] = 0.5 x 200 – 0.5 x 100 = 100 – 50 = 50美元
(牌手2在牌手1诈唬的一半时候赢得底池,在牌手1拿着AA的一半时候输掉底池。)
我们已经知道,牌手2在这个游戏中的EV应该是25美元,因此牌手1总是用QQ诈唬牌的策略是次优的,因为它给了牌手2超过其真实期望值(25美元)的更高收益(50美元)。
纳粹策略B:牌手1从不用QQ诈唬
如果牌手1从不用QQ诈唬,牌手2就没有任何理由用KK跟注,因为他总是输。
在那种情况下,牌手1将用他的AA下注并从不得到支付,而每当他拿着QQ时,牌局将以两方check且牌手2的KK摊牌获胜结束。若采用这种策略,牌手2的EV是:
EV = 0.5 x 100 = 50美元
同样,这种玩法给了牌手2超过其期望值的收益。
牌手1解决方案
我们知道牌手2将从不用KK下注,因此牌手1用AA得到价值的唯一方式是下注,但如果牌手1从不用QQ诈唬,用KK跟注将是-EV的,这意味着牌手2应该总是弃牌。如果牌手1总是用QQ诈唬,牌手2 用KK跟注将是+EV的,这意味着他应该总是跟注。
我们需要找出牌手1的最优诈唬频率,从而牌手2用KK跟注赚不到钱,也亏不到钱。换句话说,牌手1需要使牌手2对跟注或弃牌不偏不倚:
牌手2跟注的EV = 牌手2弃牌的EV
我们根据定义知道弃牌的EV是零,因此:
牌手2跟注的EV = 0
使用我们的EV公式:
EV = [%W * $W]-[%L * $R]
我们做一下参数替换:
%W = W
%L = 1 – W
$W = b + p
$R = b
[W * (b + p)] – [(1 – W)*b] = 0
这里:
B表示下注额,p表示底池大小
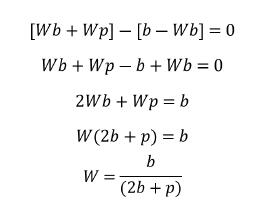
为了对跟注和弃牌不偏不倚,牌手2的获胜频率必须是:
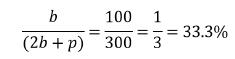
这恰好与他的底池赔率一致:

这个结果应该并不出乎意料,因为牌手2赢得底池的频率和牌手1诈唬的频率一致。我们知道,因为河牌圈不存在后续出牌,底牌赔率简单地告诉一个牌手为了不亏不盈应该用怎样的频率跟注。因此,为使牌手2对跟注和弃牌不偏不倚,牌手1必须以等于牌手2底池赔率的频率诈唬。
现在我们要做的只是找出牌手1用QQ下注的频率,从而他的下注范围是67%价值牌和33%诈唬牌。
牌手1的诈唬频率
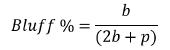
牌手1的价值下注频率
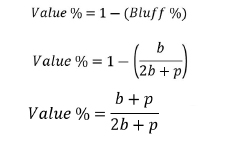
牌手1的诈唬价值比(Bluff-to-Value Ratio)

牌手1需要在他的下注范围中为他的每两个价值牌组合搭配一个诈唬牌组合,因此他应该以50%的频率用他的QQ下注。
牌手1的总下注频率
牌手1一半的时候拿着AA,并在100%的时候用它们下注:
0.5 * 100% = 50%
牌手1一半的时候拿着QQ,并在50%的时候用它们下注:
0.5 * 0.5% = 25%
总下注频率 = 用AA下注的频率 + 用QQ下注的频率 = 50% + 25% = 75%
总check频率 = 100% – 75% = 25%
牌手1的最终EV数据
AA的EV:
用AA下注的EV = (牌手2弃牌的EV * 牌手2的弃牌率) + (牌手2跟注的EV * 牌手2的跟注率) = 100 * 0.5 + 200 * 0.5 = 50 + 100 = 150美元
用AA check的EV = 底池大小 * 底池权益 = 100 * 100% = 100美元
用AA下注的EV是150美元,明显高于用它check的EV(100美元)。
AA的EV = (用AA下注的EV * AA的下注率) + (用AA check的EV * AA的check率)= 150 * 100% + 100 * 0% = 150美元
QQ的EV:
用QQ下注的EV = (100 * 0.5) + ((-100) * 0.5) = 50 – 50 = 0
QQ的EV = (用QQ下注的EV * QQ的下注率) + (用QQ check的EV * QQ的check率)= 0 * QQ的下注率 + 0 * QQ的check率 = 0
那么牌手1在这个游戏中的EV是:
EV = AA的EV * 发到AA的频率 + QQ的EV * 发到QQ的频率 = 150 * 50% + 0 * 50% = 75美元
牌手2解决方案
我们知道牌手1总是用AA下注,因此当我们check时,他们放弃用QQ诈唬。这意味着当牌手2看到牌手1 check时,他应该随后check,用KK摊牌获胜。因为牌手1总是放弃QQ,用KK下注没有任何价值。为了解决牌手2的游戏策略,我们只需要找出牌手1下注时他的策略和EV。
如果牌手2以一种1/3时候诈唬的平衡策略。
牌手2跟注的EV是:
EV = [%W * $W] – [%L * $R] = 1/3 * 200 – 2/3 * 100 = 200/3 – 200/3 = 0
如果牌手1采用纳什均衡策略,牌手2是跟注还是弃牌并不重要,因为两个行动的EV都是零。虽说如此,牌手2仍然需要以上定频率跟注,否则牌手1可以偏离平衡,通过更频繁地诈唬来剥削他。
例如,如果牌手2选择从不用KK跟注,牌手1可以开始用QQ 100%诈唬,赢得整个底池。如果牌手2选择总是用KK跟注,那么牌手1可以通过不再用QQ诈唬来剥削牌手2。
我们需要找出牌手2的最优跟注频率,从而牌手1用QQ诈唬时赚不到钱,但也不会输钱。换句话说,牌手2必须使牌手1在拿着QQ时对诈唬和check不偏不倚。
牌手1诈唬的EV = 牌手1 check的EV
我们知道牌手1用QQ check的EV为零,因为他摊牌时会输,因此:
牌手1诈唬的EV = 0
使用我们的EV公式:
弃牌的EV * 牌手2弃牌率 + 跟注的EV * 牌手2跟注率 = 0
我们做一下参数替换:
牌手2跟注率 = c
牌手2弃牌率 = 1 – c
弃牌的EV = p
跟注的EV = -b
[p * (1 – c)] + [-b * (c)] = 0
这里:
B表示下注额,p表示底池大小
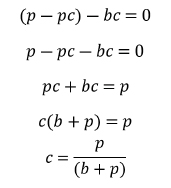
这个数字就是最低防守频率(MDF)。
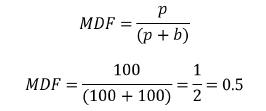
为了使牌手1拿着QQ时对诈唬和check不偏不倚,牌手2必须在50%的时候用KK跟注。解决这个问题的另一种方式是求解为使牌手1不偏不倚P2的弃牌率必须是多少。我们可以用EV公式进行计算。
弃牌的EV * 牌手2弃牌率 + 跟注的EV * 牌手2跟注率 = 0
我们做一下参数替换:
牌手2跟注率 = 1 – f
牌手2弃牌率 = f
弃牌的EV = p
跟注的EV = -b
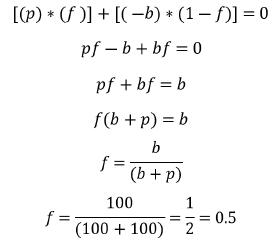
为使牌手1拿着QQ时对诈唬和check不偏不倚,P2必须在50%的时候放弃KK。
注意,b/(b + p)的值与牌手1的诈唬价值比相同。
这个数字被称作Alpha,它表示为使诈唬不亏不盈需要的诈唬成功率。在本例中,如果牌手1用QQ诈唬在超过50%的时候奏效,那么诈唬将是有利可图的。
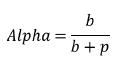
因为弃牌频率和跟注频率是互补数字,他们应该相加为1。因此,如果你知道其中一个,你总是可以轻易算出另一个。牌手1的最低防守频率也可以这样算出来:
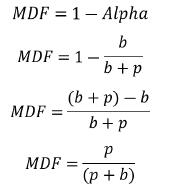
Alpha和MDF是GTO的两个关键概念,也将在书中反复用到。
牌手2的最终EV数据
牌手2跟注的EV = 0
牌手2弃牌的EV = 0
牌手2 Check的EV = 底池大小 * 牌手2的底池权益(Equity)
因为摊牌时KK总是打败QQ,牌手2对抗QQ的底池权益总是100%。
牌手2 Check的EV = 100 * 100% = 100美元
牌手1只在50%的时候用他的QQ check,因此
牌手2 check的EV = 100 * 25% = 25美元
通灵玩具游戏完整解决方案总结
底池大小:100美元
筹码深度:100美元
公共牌:3♠ 3♥ 3♣ 2♦ 2♠
牌手1: EV 75美元
AA:下注100美元(100%),Check(0%)
QQ:下注100美元(50%),Check(50%)
牌手1总下注频率:75%
牌手1总check频率:25%
牌手2:EV 25美元
对抗Check:用KK 100% check
对抗100美元下注:50%的时候用KK跟注,50%的时候弃牌
决策树(处于纳什平衡时)
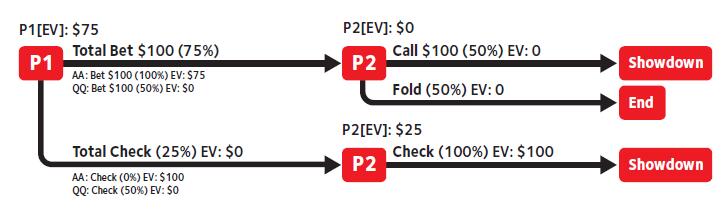
关于这个完整解决方案我们仍有两个问题需要回答。
如果调转两个牌手的位置会发生什么?
在两极化范围对抗抓诈牌的场合,位置并不重要!如果牌手2处在不利位置,他不会用Kk下注,因为那是劣势策略,因此他的纳什均衡策略应该是100% check。
牌手2在有利位置时仍然想用他的AA 100%下注,因为随后check是劣势策略,而且牌手1仍然想以b/(b + P)的频率用QQ诈唬。
牌手1的最优下注尺度是什么?
如果牌手1的范围完美两极化而牌手2的范围是紧缩的,牌手1的最优下注尺度总是全压!如我们在表10所见,牌手1的EV随着下注尺度增加而上升。这是因为,下注尺度越大牌手1就可以越频繁地诈唬。在这个游戏中,牌手2只在牌手1用QQ check的分支是赚钱的。因此,那个分支越少发生,牌手2赚到的钱就越少。所以,牌手1的EV在下注尽可能大时是最大化的。如果牌手1可以下注无穷多的资金,他将获得底池的100%份额。
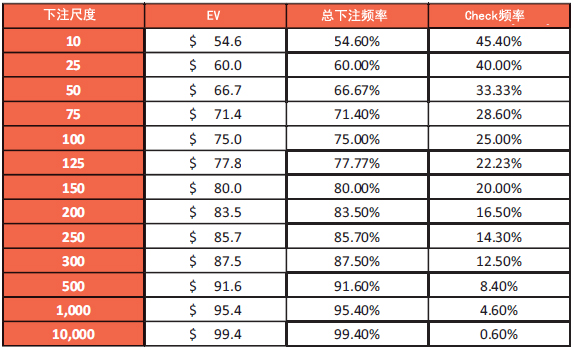
表10:牌手1取决于下注尺度的EV
天龙扑克,亚洲扑克游戏领导者!天龙扑克注册地址:http://www.tianlongqipai.com
本文由德州扑克跟我学整理发布
 博狗扑克 蜗牛扑克 德州扑克跟我学
博狗扑克 蜗牛扑克 德州扑克跟我学
















